Graficas en Tres Dimensiones
Paraboloide
Superficie tridimensional curva, o sólido formado por una parábola alrededor de su eje.
Formula:
Las secciones transversales al eje 0Z son circulares.
Observando la ecuación para cada eje:
Para el Eje XZ Para el Eje YZ
Hacemos Y= 0 Hacemos X= 0
Obtenemos: Obtenemos:
z z
x y
Para el eje XY
Hacemos z=0 o z podria tener algun vr, el que nos dirá que figura se forma.
Por lo tanto, obtenemos:
Tipos de Paraboloide:
Paraboloide Elíptico
Formula: +
Paraboloide Hiperbólico
Formura: -
Ejemplo:
Plano XZ Plano YZ
z
x y
Plano XY
Z=9
Por lo que tenemos una Circunferencia de r = 3
Con Centro = C(0,0)
y
Mostrando, Finalmente en el Pano XYZ
z
By: Andrea Rojas











Una elipsoide es una superficie cuadrática con centro de simetría.
Ecuación:
-
Con centro C(0, 0, 0) es:
-
Si centro fuera C(x0, y0, z0), entonces la ecuación sería:
En donde las constantes a, b y c son los las longitudes de los semiejes del elipsoide.
Puntos A(a, 0 ,0), A'(-a, 0, 0), B(0, b, 0), B'(0, -b, 0), C(0, 0, c) y C'(0, 0, -c).
Es decir, Extensión: -a ≤ x ≤ a; -b ≤ y ≤ b; -c ≤ z ≤ c.
Características y consideraciones:
-
El elipsoide es simétrico respecto:
-
Al origen de coordenadas.
-
A los ejes de coordenadas.
-
A los planos coordenados.
Una ecuación paramétrica de este elipsoide es:
Cuando dos de las tres constantes son iguales se trata de un esferoide y si a = b = c = r, se tiene que debemos considerar una esfera de radio r.
Las trazas del elipsoide:
Son elipses, es decir, la intersección con planos paralelos a los planos coordenados es una elipse.
Recordando:
-
Plano YZ:
-
Plano XZ:
-
Plano XY :
Curiosidades
-
En la antigüedad el elipsoide no era considerado, se tomaba como una esfera deformada.
-
Halley, en 1705, demostró que el cometa que ahora lleva su nombre trazaba una órbita elíptica alrededor del Sol.
-
Poco después, Galileo Galilei (1564-1642) probó esta teoría realizando los cálculos necesarios y la utilización de un telescopio desarrollado por él mismo.
-
Un balón de rugbyes un elipsoide de revolución, es decir una elipse girando.
El siguiente video será de gran utilidad, en cuanto a los pasos para graficar la superficie a partir de la ecuación dada:
By: Maria Puertas








Cilindro
Elipsoide
Una gráfica es el nombre de un conjunto de puntos que se plasman en coordenadas cartesianas y sirven para analizar el comportamiento de un proceso o un conjunto de elementos o signos que permiten la interpretación de un fenómeno.
Al saber que es una gráfica debemos también saber qué es lo que buscamos graficar en este caso especifico aprenderemos como se grafica un cilindro por lo cual debemos conocer su definición que dice que: En geometría, un cilindro es una superficie de las denominadas cuádricas formada por el desplazamiento paralelo de una recta llamada generatriz a lo largo de una curva plana, denominada directriz del cilindro.
Paso_1. Identificar El Tipo De Cilindro: Ya al conocer que vamos a hacer y también que es lo que queremos graficar podemos comenzar observando su fórmula general que en el caso de los cilindros existen diferentes tipos los cuales son:
-
Cilindro Elíptico
-
Cilindro Parabólico
-
Cilindro Hiperbólico
Paso_2. Observar Como Es La Gráfica Sin Tener En Cuenta “Z”: Lo primero que se debe notar es que cada una de las formulas sin la variable “Z” es un tipo de grafica él es plano “XY” por lo cual podemos entes de graficar en el espacio podemos ver que figura se genera en el plano y de allí diremos que la variable “Z” es toda la zona por la cual se moverá la gráfica del plano.
Ejemplos:
-
Cilindro Elíptico: en este caso la gráfica que se refleja en el plano es el de una circunferencia o una elipse por lo cual en el plano se vería de esta forma:
-
Cilindro Parabólico: aquí observaremos la gráfica de una parábola que es la siguiente:
-
Cilindró Hiperbólico: el este caso la gráfica que se genera en el plano es el de una hipérbola como la siguiente:
Paso_3. Darle los valores a “Z” y llevar la gráfica al espacio R3: aquí lo que haremos es utilizar los datos que anteriormente obtuvimos y los emplearemos en comenzar a graficar nuestra ecuación para esto si utilizaremos la variable “Z”.
-
Cilindro Elíptico: este nos debería quedar de la forma siguiente:
-
Cilindro Parabólico: el debería tener la forma de medio cilindro elíptico:
-
Cilindro hiperbólico: este es similar al parabólico solo que posee dos de estos contra opuestos:
By: Jiuder Guillen







Esfera
Una esfera es un semicírculo que gira sobre su diámetro y que describe en el espacio un cuerpo geométrico llamado esfera.
Si consideramos una semicircunferencia que gira sobre su diámetro, la superficie curva que se genera es la superficie esférica.
Elementos de una esfera:
Centro: Punto interior que equidista de cualquier punto de la esfera.
Radio: Distancia del centro a un punto de la esfera.
Cuerda: Segmento que une dos puntos de la superficie.
Diámetro: Cuerda que pasa por el centro.
Polos: Son los puntos del eje de giro que quedan sobre la superficie esférica.
Area y Volumen
para calcular el area de una esfera se utiliza:
para calcular el volumen de una esfera se utiliza:
Circunferencias en una esfera
Paralelos: Circunferencias obtenidas al cortar la superficie esférica con planos perpendiculares al eje de revolución.
Ecuador: Circunferencia obtenida al cortar la superficie esférica con el plano perpendicular al eje de revolución que contiene al centro de la esfera.
Meridiano: Circunferencias obtenidas al cortar la superficie esférica con planos que contienen el eje de revolución.
Hemisferio
Es cada una de las partes en que queda dividida la superficie esférica por un plano que pasa por el centro de la esfera, llamado plano diametral.
Semiesfera
Parte de una esfera comprendida entre dos planos que se cortan en el diámetro de aquella.
Huso esférico
Parte de la superficie de una esfera comprendida entre dos planos que se cortan en el diámetro de aquella.
Cuña esférica
Parte de de una esfera comprendida entre dos planos que se cortan en el diámetro de aquella.
Aréa del huso esferico y volumen de la cuña esferica
Para el calculo del area se utiliza
Para el calculo del volumen se utiliza
Casquete esférico
Es cada una de las partes de la esfera determinada por un plano secante.
Aréa y volumen del Casquete esférico
Para el calculo del area se utiliza
Para el calculo del volumen se utiliza
Para el calculo del radio de la esfera se utiliza
Zona esférica
Es la parte de la esfera comprendida entre dos planos secantes paralelos.
Aréa y volumen de la zona esferica
Para el calculo del area se utiliza
Para el calculo del volumen se utiliza
By: José Navarro












Hiperboloide
Un elipsoide es una superficie curva cerrada cuyas tres secciones ortogonales principales son elípticas, es decir, son originadas por planos que contienen dos ejes cartesianos.
En matemáticas, es una cuádrica análoga a la elipse, pero en tres dimensiones.
Un elipsoide se obtiene al deformar una esfera, mediante una transformación homológica, en la dirección de sus tres diámetros ortogonales.
Si el centro de simetría es C (0, 0, 0), y el eje del hiperboloide es el eje z, entonces la ecuación del hiperboloide de una hoja es:
en donde una sola de las variables es negativa
y la ecuación del hiperboloide de dos hojas es:
en donde dos de las variables son negativas
Cuando la hiperbola no se encuentra en el origne, sus ecuaiones serian
En una hoja:
y su grafica es:
En dos hojas:
Su grafica es:
Ahora a continuación un pequeño ejemplo de como graficar un hiperboloide:
Se nos presenta el siguiente caso:
En donde:
a=4; b=3; c=5
Graficando en el plano XY:
-
tenemos una elipse
-
Haciendo z=0,obtenemos esto:
Donde a=4; b=3
Y la grafica de esta elipse sería así:
Graficando en el plano YZ:
-
Tenemos una hipérbola
-
Haciendo x=0,obtenemos esto:
En donde la grafica de esta hipérbola sería así:
Graficando en el plano XZ:
-
Tenemos una hipérbola
-
Haciendo y=0,obtenemos esto:
En donde la grafica de esta hipérbola sería así:
Uniendo los tres planos quedaria así:
By: Jhohanderly Blanco






Cono
Definición de cono
Es el cuerpo de revolución obtenido al hacer girar un triángulo rectángulo alrededor de uno de sus catetos.
Formula
Su fórmula es:
X2 + Y2 = Z2
¿Cómo identificarlo?
De acuerdo a la formula como se ve, tiene X2, que eso es una parábola de allí que se puede suponer pero luego se ve que se le suma Y2, recordando formulas eso sería la de circunferencia y la formula de circunferencia es X2 + Y2 = r2, es muy parecida pero lo más importante es que tiene un vector en Z2, es de allí que uno puede pensar que será la de circunferencia pero no, la formula de la esfera es X2 + Y2 + Z2 = r2, excepto que no hay ninguna r (radio) y la Z va positiva después del igual.
Graficación
Vamos a graficar en cada lado del plano
Graficación en el Plano XZ
Plano XZ ; cuando Y=0
X2+ Y2 = Z2
=> X2 = Z2
Graficación en el Plano ZY
Plano YZ ; cuando X=0
X2+ Y2 = Z2
=> Y2 = Z2
Graficación en el Plano XY
Plano XY ; cuando Z=0
X2+ Y2 = Z2 => X2+ Y2 = 0
Podemos hacer en este caso dos cosa
1.- Recordar que la formula de circunferencia es r2 = X2+ Y2; podemos cambiar X2+ Y2 por r2 así:
-
X2+ Y2 = 0
-
r2 = 0
Centro(0,0)
2.- O podemos despejar X o Y:
Esto sería lo mismo en Y
Graficación en el Plano XYZ
En todo el Plano XYZ
X2+ Y2 = Z2
Vista superior del cono
La vista superior del cono es igual a una circunferencia
Ejemplo
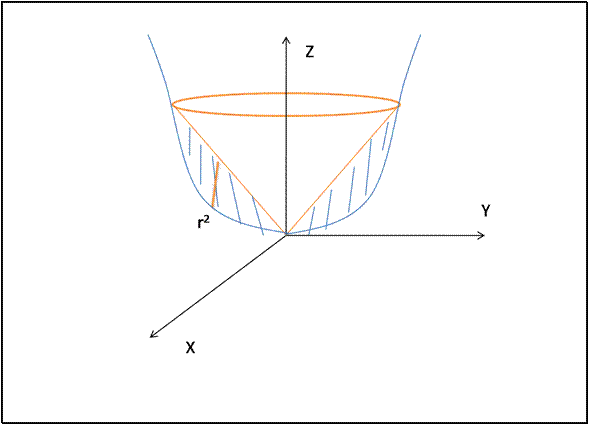
Buscar el volumen del cono comprendido de Z=√(X2+Y2) y Z= X2+Y2
1.- paso uno grafica el dibujo
Ahora hacemos la grafica de la vista superior de la figura
2.- paso 2 ahora igualamos la dos formulas en X2+Y2
-
Z=√Z
-
-
-
Z=1
-
Z=0
Ya tenemos los primeros limites, ahora tenemos que decidir si hacerlo normal o por coordenadas polares
En mi caso lo hare por coordenadas polares
Donde Z = r
En coordenadas polares los limites de una circunferencia van de 0 a 2π (estos serian los segundos limites), ya que estamos tomando todo el circulo
Ahora cambiamos las Z por r
3.- Paso 3 resolvemos el ejercicio
By: Arturo Vielma