Integrales Dobles

Al igual que la integral de una función de una variable representa el área (con signo) de la región bajo la gráfica de dicha función, la integral de una función de dos variables sobre una región representa el volumen del espacio que queda entre la gráfica (tridimensional) de la función y el plano sobre el cual la dibujamos. La integral en una cierta región de una función de dos variables se llama integral doble.

Sea z=f(x;y) una función definida, continua y acotada en una región R del plano. Consideremos un punto Pm arbitrario interior a cada sub-divisiónde una partición Pm y sea f(Pm) el valor de la función en dicho punto.

Llamaremos con el nombre de suma de productos interiores o suma de Riemann correspondientes a la función f(x;y) y a una partición P, a:

Si efectuáramos nuevas particiones de la región R, cada vez más refinadas tal que Δ tienda a 0 aumentaría el número de partes.

Si existe el límite de esta suma, cuando lo llamaremos“Integral Doble” de la función en la región R y lo representamos por:

R se denomina dominio de integración.

Propiedades de la Integral Doble:

Descomposición con respecto de la región de integración:

Si la región R se descompone en

2. Propiedad de Homogeneidad:

Siendo C = constante y integrable en R.

3. Descomposición con respecto al integrando:

Siendo son integrables sobre la región R

4. Propiedad de monotonía:

5. Si son integrables en R y:

Interpretación gráfica:

La integral doble de una función no negativa en dos variables se interpreta como el volumen bajo la superficie z = f(x,y) y sobre la región R del plano xy.

Cálculo de integrales dobles:

La integral doble de f sobre la región R, está dada por el valor común de las dos integrales iteradas.

Donde a, b, c y d son los límites de integración de la región R.

Para resolver la integral doble, se mantiene fija una variable y se integra con respecto a la otra variable.

Límites de integración:

Secciones transversales verticales:

La región R está limitada por las gráficas de g1 y g2 en el intervalo [a, b]. Si R es descrita por:

2.Secciones transversales horizontales :

La región R está limitada por las gráficas de h1 y h2 en el intervalo [c, d]. Si R es descrita por:

By: Alejandro Perez

Centro de Masa

Conociendo las integrales dobles, podemos considerar una lámina con densidad variable. Supongamos que la lámina ocupa una región D del plano xy y su densidad (en unidades de masa por área unitaria) en un punto (x,y) en D está dada por ρ(x,y), donde ρ es una función continua en D. Esto significa que:

Donde Δm y ΔA son la masa y el área de un pequeño rectángulo que contiene a (x,y), y el límite se toma cuando las dimensiones del rectángulo se aproximan a 0. Para hallara la masa total m de la lámina, dividimos el rectángulo R que contiene a D, en sub-rectángulos Rij del mismo tamaño y consideramos que ρ(x,y) es 0 fuera de D. Si escogemos un punto (x*ij,y*ij) de Rij, entonces la masa de la parte de la lámina que ocupa Rij es aproximadamente ρ(x*ij,y^ij)^ΔA , donde ΔA es el área de R(x*ij,y*ij). Si sumamos todas estas masas, obtenemos una aproximación a la masa total:

Si ahora aumentamos el número de sub-rectángulos, obtenemos la masa total m de la lámina como el límite del valor de las aproximaciones:

Sea f(x,y) la función de densidad (masa por unidad de área) de una distribución de masa en el plano xy Entonces la masa total de un trozo plano R es:

El centro de gravedad de la masa del trozo plano anterior tiene coordenadas donde:

Los momentos de inercia de Ix e Iy de la masa de R con respecto a los ejes x e y respectivamente son:

Ejemplo 1:

Ejemplo 2:

Ejemplo 3:

Video Explicativo:

By: Melvin Sorzano

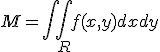
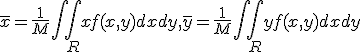
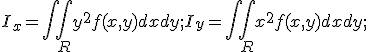
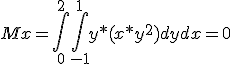
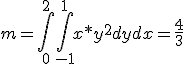
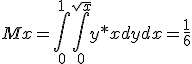
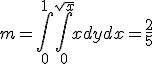
Cambio de coordenadas cartesianas a polares

Ejemplo 1:

Ejemplo 2:

By: Carolina Abad

Calculo de Volumen

Al igual que las integrales de una variable sirven para calcular el área bajo una gráfica, las integrales dobles sirven para calcular volúmenes. Concretamente, cuando F ≥ 0, la integral el volumen bajo la gráfica en el rectángulo [a, b] × [c, d], esto es, a ≤ x ≤ b, c ≤ y ≤ d.

Lo mismo se cumple en regiones más generales. Es decir, si R es una región del plano y F = F (x, y) es una función no negativa en ella, entonces

(1)

Si F = 1, entonces como el volumen es el área de la base por la altura (uno en este caso)

(2)

Para dotar de significado a F hay que transformarla en una integral iterada como las de antes con unos límites específicos. Para ello podemos dividir la región R en “rodajas”(secciones) verticales u horizontales.

En el primer caso la x variará entre dos números (la abscisa de la primera y la última sección) y la y variará entre las gráficas de las funciones que limitan inferior y superiormente la región. Debemos entonces integrar primero en y para tener en cuenta la contribución de cada sección.

De la misma forma, cuando la región R está limitada a la izquierda y a la derecha por dos gráficas sencillas x = g1(y), x = g2(y), puede ser más cómodo considerar secciones horizontales. En este caso la y será la que varíe entre dos números.

Cualquiera de los dos métodos debe dar el mismo resultado. En algunos casos, se necesita una subdivisión de la región para aplicarlos. Por ejemplo, si quisiéramos integrar una región con forma de estrella, sería conveniente dividirla en triángulos, calcular las integrales sobre cada uno de ellos y sumar los resultados, porque una estrella no está directamente limitada por dos gráficas.

Ejemplo. Calculemos el volumen limitado por F (x, y) = 2 − x + y (esto es un plano) y por el círculo unidad C en el plano XY . Si utilizamos la estrategia de considerar secciones verticales en C, presentaremos el círculo unidad como

De acuerdo con (1), el volumen viene dado por:

La última integral es un poco complicada y nos vamos a ayudar de que sabemos que

Porque esta integral de una variable es el área del semicírculo de radio 1 (área del círculo = πR2). Entonces la integral anterior es:

Video Explicativo

By: Yorwill Torres